Backpropagation of a vanilla RNN
This post investigates how to code up a vanilla RNN. Most of the code and example are copied from Andrej Karpathy’s blog:
The backpropagation is clearly derived by the Chain rule in calculus.
Character-Level Language Models
For instance, we use the vanilla RNN to generate the next character in the world ‘‘hello’’, which is a character-level language model. The forward pass is illustrated in the following diagram. From the diagram, one can see that this RNN is a many-to-many model, where we have the one hot encoder of ‘h’, ‘e’, ‘l’, ‘l’ as input sequence and the four vectors of probability of ‘h’, ‘e’, ‘l’, ‘o’ as output. The loss function is the summation of 4 cross entropies since we totally make four predictions.

Initialize parameters
As in the forward pass, we have three weight matrics, \(W_{xh}, W_{hh}, W_{hy}\) and two bias vectors, \(b_{h}, b_{y}\) , to learn. The weight matrics are randomly initialized and bias vectors are initialized to be 0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class vanillaRNN:
def __init__(self, n_x, n_h, seq_length, learning_rate):
# hyperparameters
self.n_x = n_x
self.n_h = n_h
self.seq_length = seq_length
self.learning_rate = learning_rate
# initialize model parameters
self.Wxh = np.random.randn(n_h, n_x) * 0.01
self.Whh = np.random.randn(n_h, n_h) * 0.01
self.Why = np.random.randn(n_x, n_h) * 0.01
self.bh = np.zeros((n_h, 1))
self.by = np.zeros((n_x, 1))
# memory vars for adagrad
self.mWxh = np.zeros_like(self.Wxh)
self.mWhh = np.zeros_like(self.Whh)
self.mWhy = np.zeros_like(self.Why)
self.mbh = np.zeros_like(self.bh)
self.mby = np.zeros_like(self.by)
Forward pass
The simple RNN model replicates one neuron for seq_length times, with the same wight and bias parameter. The neuron has the previous hidden units and the new input as input information, and output the predicted y and the updated hidden units.
\[\begin{align} h_t & = \text{tanh}(W_{hh}h_{t-1} + W_{xh}x_t +b_h) \\ y_t & = W_{hy}h_{t} + b_y \\
p_t & = \frac{e^{y_t}}{\sum_{i = 1}^{n_y} e^{y_{t, i}}} \\
l_t & = -\sum_{i = 1}^{n_y} z_{t, i}\text{log}(p_{t, i}) \\
L & = \sum_{t = 1}^{n_{seq}}l_t \end{align}\]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def forward_pass(self, inputs, targets, hprev):
"""
inputs -- list of integers (tokenizer: char to int)
targets -- list of integers (tokenizer: char to int)
hprev -- the initial hidden state
"""
x, h, y, p = {}, {}, {}, {}
h[-1] = np.copy(hprev)
loss = 0
for t in range(len(inputs)):
# one hot encoder of a char
x[t] = np.zeros((self.n_x, 1))
x[t][inputs[t]] = 1
h[t] = np.tanh(self.Wxh @ x[t] + self.Whh @ h[t-1] + self.bh)
y[t] = self.Why @ h[t] + self.by
p[t] = np.exp(y[t]) / np.sum(np.exp(y[t]))
loss = loss - np.log(p[t][targets[t], 0])
return loss, x, h, p
Backpropagation
Backpropagation in the neural network is an application of chain rule in calculus. I write down the detailed derivation of the partial derivatives of the parameters.
\[dW_{hy} = \frac{\partial L}{\partial W_{hy}} = \sum_{t = 1}^{n_{seq}} \frac{\partial l_t}{W_{hy}},\text{ where }\] \[\begin{align} \frac{\partial l_t}{W_{hy}^{[i, :]}} & = \frac{\partial l_t}{\partial p_{t, j}}\frac{\partial p_{t, j}}{y_{t, i}}\frac{\partial y_{t, i}}{\partial W_{hy}^{[i, :]}}, \text{ where } j = \arg_i\{z_{t, i} = 1\} \\
& = -\frac{1} {p_{t, j}} \left\{\begin{array}{lr} (p_{t, j} - p_{t, j}^2)h_t^T & i = j \
-(p_{t, i}p_{t,j})h_t^T & i \neq j\end{array}\right. \end{align}\] Therefore, \[\begin{align}\frac{\partial l_t}{W_{hy}} & = \frac{\partial l_t}{y_t}\cdot h_t^T = (p_t - e_j)\cdot h_t^T \\
\frac{\partial l_t}{b_{y}} & = \frac{\partial l_t}{y_t} = (p_t - e_j) \end{align}\]
\[\begin{align}dW_{hh} = \frac{\partial L}{\partial W_{hh}} & = \sum_{t = 1}^{n_{seq}}\frac{\partial L}{\partial h_t}\frac{\partial h_t}{\partial W_{hh}}, \text{ set }h_{t}^{raw} = W_{hh}h_{t-1} + W_{xh}x_t +b_h \\
& = \sum_{t = 1}^{n_{seq}}\frac{\partial L}{\partial h_t}\frac{\partial h_t}{\partial h_{t}^{raw}}\frac{\partial h_t^{raw}}{\partial W_{hh}} \\
& = \sum_{t = 1}^{n_{seq}}\frac{\partial L}{\partial h_t}(1 - h_t^2)h_{t-1}^T, \text{ since }\frac{d}{dx} \text{tanh}(x)= 1-\text{tanh}^2(x). \end{align}\] Similarly, \[\begin{align}dW_{xh} & = \sum_{t = 1}^{n_{seq}}\frac{\partial L}{\partial h_t}(1 - h_t^2)x_{t}^T\\
db_h & = \sum_{t = 1}^{n_{seq}}\frac{\partial L}{\partial h_t}(1 - h_t^2). \end{align}\] Now, it remains to compute \[\begin{align}\frac{\partial L}{\partial h_t} & = \frac{\partial L}{\partial y_t}\frac{\partial y_t}{\partial h_t} + \frac{\partial L}{\partial h_{t+1}} \frac{\partial h_{t+1}}{\partial h_t} \\
& = \frac{\partial l_t}{\partial y_t}\frac{\partial y_t}{\partial h_t} + \frac{\partial L}{\partial h_{t+1}} \frac{\partial h_{t+1}}{\partial h_{t+1}^{raw}} \frac{\partial h_{t+1}^{raw}}{\partial h_t}\\
& = W_{hy}^Tdy_t + \frac{\partial L}{\partial h_{t+1}}(1-h_{t+1}^2)\frac{\partial h_{t+1}^{raw}}{\partial h_t} \\
& = W_{hy}^Tdy_t + W_{hh}^T(1-h_{t+1}^2)\frac{\partial L}{\partial h_{t+1}}. \end{align}\]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def backpropagation(self, x, h, p, targets):
dWxh, dWhy, dWhh = np.zeros_like(self.Wxh), np.zeros_like(self.Why), np.zeros_like(self.Whh)
dbh, dby = np.zeros_like(self.bh), np.zeros_like(self.by)
dhnext = np.zeros_like(h[0])
for t in reversed(range(self.seq_length)):
dy = np.copy(p[t])
dy[targets[t]] = dy[targets[t]] - 1
dWhy = dWhy + dy @ h[t].T
dby = dby + dy
dh = self.Why.T @ dy + dhnext
dhraw = (1 - h[t] * h[t]) * dh
dbh = dbh + dhraw
dWxh = dWxh + dhraw @ x[t].T
dWhh = dWhh + dhraw @ h[t-1].T
dhnext = self.Whh.T @ dhraw
for dpara in [dWxh, dWhh, dWhy, dby, dbh]:
np.clip(dpara, -5, 5, out = dpara)
return dWxh, dWhh, dWhy, dbh, dby
An example
Andrej Karpathy provides a small Shakespeare data set. We set n_h = 100 and seq_length = 25 in the vanilla RNN. After 50000 iterations, the loss function can not furthur decrease. 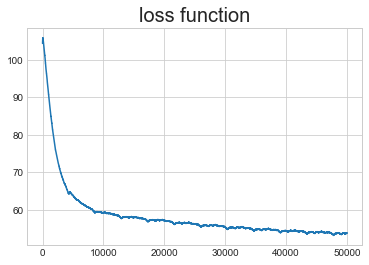
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
def update_para(self, dWxh, dWhh, dWhy, dbh, dby):
for para, dpara, mem in zip(['Wxh', 'Whh', 'Why', 'bh', 'by'],
[dWxh, dWhh, dWhy, dbh, dby],
['mWxh', 'mWhh', 'mWhy', 'mbh', 'mby']):
setattr(self, mem, getattr(self, mem) + dpara * dpara)
setattr(self, para, getattr(self, para) - self.learning_rate * dpara/np.sqrt(getattr(self, mem) + 1e-8))
def train(self, inputs, char_to_int, int_to_char, max_iter = 1e4):
iter_num, position = 0, 0
loss_list = []
loss_list.append(- np.log(1 / self.n_x) * self.seq_length)
while iter_num <= max_iter:
if iter_num%1000 ==0: print(iter_num)
## reset the rnn after an epoch
if position + self.seq_length + 1 >= len(inputs) or iter_num == 0:
hprev = np.zeros((self.n_h, 1))
position = 0
## chars to int
input_bacth = [char_to_int[ch] for ch in inputs[position:position + self.seq_length]]
target_bacth = [char_to_int[ch] for ch in inputs[position + 1 : position + self.seq_length + 1]]
position = position + seq_length
## forward_pass
loss, x, h, p = self.forward_pass(input_bacth, target_bacth, hprev)
loss_list.append(loss_list[-1] * 0.999 + loss * 0.001)
## backpropagation
dWxh, dWhh, dWhy, dbh, dby = self.backpropagation(x, h, p, target_bacth)
## adagrad upate
self.update_para(dWxh, dWhh, dWhy, dbh, dby)
hprev = h[self.seq_length - 1]
iter_num = iter_num + 1
## make a sample after training
sample_ix = self.make_sample(hprev, target_bacth[-1], 200)
sample_char = ''.join(int_to_char[ix] for ix in sample_ix)
return loss_list, sample_char
def make_sample(self, hprev, seed_ix, n):
"""
sample a length n sequence from the model
"""
x = np.zeros((self.n_x, 1))
x[seed_ix] = 1
ixes = []
h = np.copy(hprev)
for t in range(n):
h = np.tanh(self.Wxh @ x + self.Whh @ h + self.bh)
y = self.Why @ h + self.by
p = np.exp(y) / np.sum(np.exp(y))
ix = np.random.choice(range(self.n_x), p = p.ravel())
x = np.zeros((self.n_x, 1))
x[ix] = 1
ixes.append(ix)
return ixes
A length 200 sample is generated from the trained RNN.
1
2
3
4
5
6
7
8
9
with open('input.txt') as f:
words = f.read()
chars = list(set(words))
words_size, vocab_size = len(words), len(chars)
char_to_int = {ch:i for i, ch in enumerate(chars)}
int_to_char = {i:ch for i, ch in enumerate(chars)}
rnn = vanillaRNN(n_x = vocab_size, n_h = 100, seq_length = 25, learning_rate = 1e-1)
loss_list, sample_char = rnn.train(words, char_to_int, int_to_char, max_iter = 50000)
1
2
3
4
5
6
7
8
9
kmmatody: nomels bake tho pav.
M:
Atw: and I; thou onsel swere, lo! meroses ssseme noke shy ust but ker, woncter id imire ghy.
What Thes hereth:
Iss:
Drou wort, netesteme here to whont toy,
All My
