Entropy and mutual information

In statistical community, one of the primary estimation methods is maximum log-likelihood estimation (MLE). However, in machine learning/engineering, log-likelihood function has been renamed as cross entropy. This post is a summary of the chapter 2 in Elements of Information Theory.

An example

We start with an example. Let X be a random variable taking values a, b, c, d with probability 1/2, 1/4, 1/8, 1/8 respectively. We would like to know the minimum expected number of binary questions required to determine the value of X. An efficient asking strategy will be asking 1) is X = a? 2) is X = b? 3) is X = c? sequentially. Therefore, the number of questions required is \[1\times 1/2 + 2\times 1/4 + 3\times(1/8+1/8) = 1.75 = H(X).\]

What if the probability distribution changes to 1/4, 1/4, 1/4 and 1/4? Then the number of questions required is \[1\times 1/4 + 2\times 1/4 + 3\times(1/4+1/4) = 2.25.\]

Actually, the minimum expected number of binary questions required to determine \(X\) lies between \(H(X)\) and \(H(X) + 1\). Entropy, \(H(X)\), is a measure of the uncertainty of a random variable; it is a measure of the amount of information required on the average to describe the random variable.

Definition of Entropy

Definition: The entropy \(H(X)\) of a discrete random variable \(X\) is defined by \[H(X) \text{ or } H(p) = -\Sigma_{x\in\mathcal{X}} p(x) \log p(x) = E_p\log \frac{1}{p(X)} \geq 0.\] The log is to the base 2 and entropy is expressed in bits. Note that \(0\log 0 = 0\). If we denote the \(H_b(X) = -\Sigma_{x\in\mathcal{X}} p(x) \log_b p(x)\), we have \(H_b(X) = (\log_ba)H_a(X)\).

Definition: The joint entropy \(H(X, Y)\) of a pair of discrete random variable \(X, Y\) with a joint distribution \(p(x, y)\) is defined as \[H(X, Y) = -\Sigma_{x\in\mathcal{X}}\Sigma_{y\in\mathcal{Y}}p(x, y)\log p(x, y) = -E\log p(X, Y).\]

Definition: If \((X, Y)\sim p(x, y)\), the conditional entropy \(H(Y|X)\) is defined as \[\begin{align} H(Y|X) & =\Sigma_{x\in\mathcal{X}}p(x)H(Y|X = x)\\
& = -\Sigma_{x\in\mathcal{X}}p(x)\Sigma_{y\in\mathcal{Y}}p(y|x)\log p(y|x)\\
& = -\Sigma_{x\in\mathcal{X}}\Sigma_{y\in\mathcal{Y}}p(x, y)\log p(y|x)\\
& = -E\log p(Y|X). \end{align}\]

Definition: The relative entropy or Kullback-Leibler distance between two probability mass functions \(p(x)\) and \(q(x)\) is defined as \[D(p||q) = \sum_{x\in\mathcal{X}}p(x)\log \frac{p(x)}{q(x)} = E_P\log\frac{p(X)}{q(X)}.\] We use the convention that \(0\log \frac{0}{q} = 0\), \(0\log\frac{0}{q} = 0\) and \(p\log\frac{p}{0} = \infty\). It is not a true distance between distributions since it is not symmetric and does not satisfy the triangle inequality. \(D(p||q)\) is a measure of the inefficiency of assuming that the distribution is \(q\) when the true distribution is \(p\).

Definition: Consider two random variables \(X\) and \(Y\) with a joint probability mass function \(p(x, y)\) and marginal probability mass functions \(p(x)\) and \(p(y)\). The mutual information \(I(X;Y)\) is the relative entropy between the joint distribution and the product distribution \(p(x)p(y):\) \[\begin{align} I(X;Y) & = \sum_{x\in\mathcal{X}}\sum_{y\in\mathcal{Y}}p(x, y)\log\frac{p(x, y)}{p(x)p(y)}\\
& = D(p(x, y)||p(x)p(y))\\
& = E_{p(x, y)}\log \frac{p(X, Y)}{p(X)p(Y)}. \end{align}\] Mutual information measures the amount of information that one random variable contains about another random variable. It is the reduction in the uncertainty of one random variable due to the knowledge of the other.

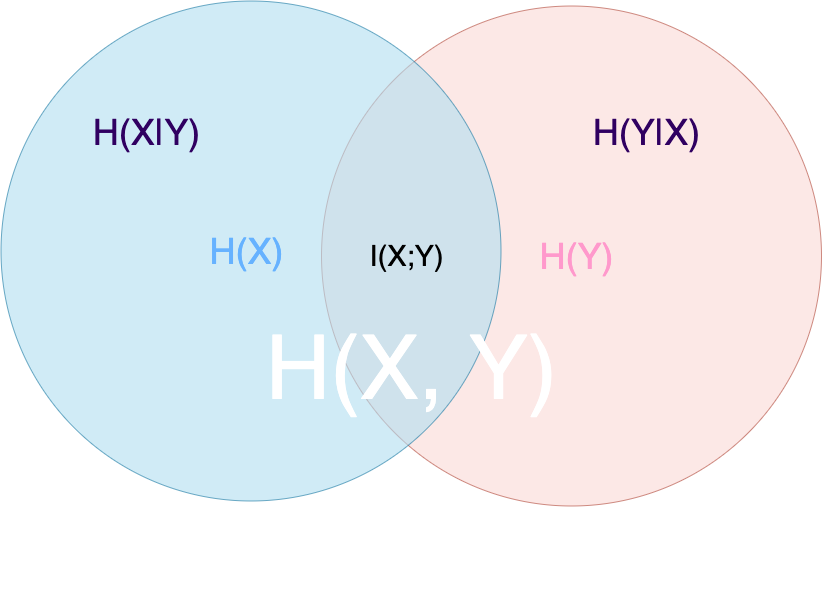
relationship and theorems

1. Chain rule \[\begin{align} H(X, Y) & = H(X) + H(Y|X)\\
   H(X, Y|Z) & = H(X|Z) + H(Y|X, Z)\\
   H(X_1, X_2, \dots, X_n) & = \Sigma_{i = 1}^n H(X_i|X_{i-1}, \ldots, X_1) \end{align}\] Note that \(H(Y|X)\neq H(X|Y)\) but \(H(X) - H(X|Y) = H(Y) - H(Y|X).\)
2. X says as much about as Y as Y says about X \[\begin{align} I(X;Y) &= H(X) - H(X|Y) = H(X) + H(Y) -H(X, Y) \\
   I(X;Y) &= H(Y) - H(Y|X)\\
   I(X;X) &= H(X) - H(X|X) = H(X) \end{align}\]
3. infomation inequality \[D(p||q)\geq 0 \] with equality if and only if \(p(x) = q(x)\) for all \(x\). (this can be proved by Jensen’s inequality since log(x) is concave.)
4. Nonnegativity of mutual information For any two random variable, \(X, Y\), \[I(X;Y)\geq 0 \] with equality if and only if \(X\) and \(Y\) are independent.
5. maximum entropy \[H(X)\leq\log|\mathcal{X}|,\] where \(|\mathcal{X}|\) denotes the number of elements in the range of \(X\), with equality if and only if \(X\) has a uniform distribution over \(\mathcal{X}\).
6. Conditioning reduces entropy, information can’t hurt \[H(X|Y)\leq H(X)\] Intuitively, the theorem says that knowing another random variable \(Y\) can only reduce the uncertanty in \(X\). But this is only true on the average. Specifically, \(H(X|Y= y)\) may be greater than or less than or equal to \(H(X)\).
7. Independence bound on entropy
   Let \(X_1, X_2, \ldots, X_n\) be drawn according to \(p(x_1, x_2, \ldots, x_n)\). Then \[H(X_1, X_2, \ldots, X_n)\leq \sum_{i = 1}^n H(X_i)\] with equality if and only if the \(X_i\) are independent.

Concavity of entropy

First, we introduce the log sum inequality.
For nonnegative numbers, \(a_1, a_2, \ldots, a_n\) and \(b_1, b_2, \ldots, b_n\), \[\sum_{i = 1}^n a_i\log\frac{a_i}{b_i}\geq \left(\sum_{i=1}^n a_i \right) \log \frac{\Sigma_{i = 1}^n{a_i}}{\Sigma_{i = 1}^nb_i}\] with equality if and only if \(\frac{a_i}{b_i} = \) const.

By using the log sum inequality, we can prove the following theorems.

1. Convexity of relative entropy
   \(D(p||q)\) is convex in the pair \((p, q)\); that is, if \((p_1, q_1)\) and \((p_2, q_2)\) are two pairs of probability mass functions, then \[D(\lambda p_1 + (1-\lambda)p_2 || \lambda q_1 + (1-\lambda)q_2) \leq \lambda D(p_1||q_1) + (1-\lambda)D(p_2||q_2)\] for all \(0\leq \lambda\leq 1\).
2. Concavity of entropy
   \(H(p)\) is a concave function of \(p\) since \(H(p) = \log|\mathcal{X}| - D(p||u),\) where \(u\) is the uniform distribution on \(|\mathcal{X}|\) outcomes.
3. Concavity and convexity of mutual information
   Let \((X, Y)\sim p(x,y) = p(x)p(y|x)\). The mutual information \(I(X; Y)\) is a concave function of \(p(x)\) for fixed \(p(y|x)\) and a convex function of \(p(y|x)\) for fixed \(p(x)\).

Fano’s inequality

Fano’s inequality relates the probability of error in guessing the random variable \(X\) to its conditional entropy \(H(X|Y)\). The conditional entropy of a random variable \(X\) given another random variable \(Y\) is zero if and only if \(X\) if a function of \(Y\) so that \(X\) become deterministic given \(Y\). Hence we can estimate \(X\) from \(Y\) with zero probability of error if and only if \(H(X|Y) = 0.\)

Extending this argument, we expect to be able to estimate \(X\) with a low probability of error only if the conditional entropy \(H(X|Y)\) is small. Fano’s inequality quantifies this idea. Suppose we use a function \(g(Y)\) as the estimator \(\hat{X}\) to estimate \(X\) and define the probability of error \[P_e = \text{Pr} (\hat{X}\neq X).\] Theorem (Fano’s inequality) For any estimator \(\hat{X}\) as a function of \(Y\), we have \[H(P_e) + P_e\log|\mathcal{X}| \geq H(X|\hat{X}) \geq H(X|Y).\] This inequality can be weakened to \[1 + P_e\log|\mathcal{X}| \geq H(X|Y).\] Corollary For any two random variable \(X\) and \(Y\), let \(p = \text{Pr} (X\neq Y)\). \[H(p) + p\log|\mathcal{X}|\geq H(X|Y).\] Theorem (information in independent copy) If \(X\) and \(X’\) are i.i.d with entropy \(H(X)\), \[\text{Pr}(X = X’) \geq 2^{-H(X)}.\] Corollary Let \(X, X’\) be independent with \(X\sim p(x), X’\sim r(x), x, x’\in \mathcal{X}.\) Then \[\begin{align} \text{Pr} (X = X’) & \geq 2^{-H(p)-D(p||r)}\\
\text{Pr} (X = X’) & \geq 2^{-H(r) - D(r||p)}. \end{align}\]