Kosaraju's algorithm to find SCCs

Definition of Strongly Connected Components

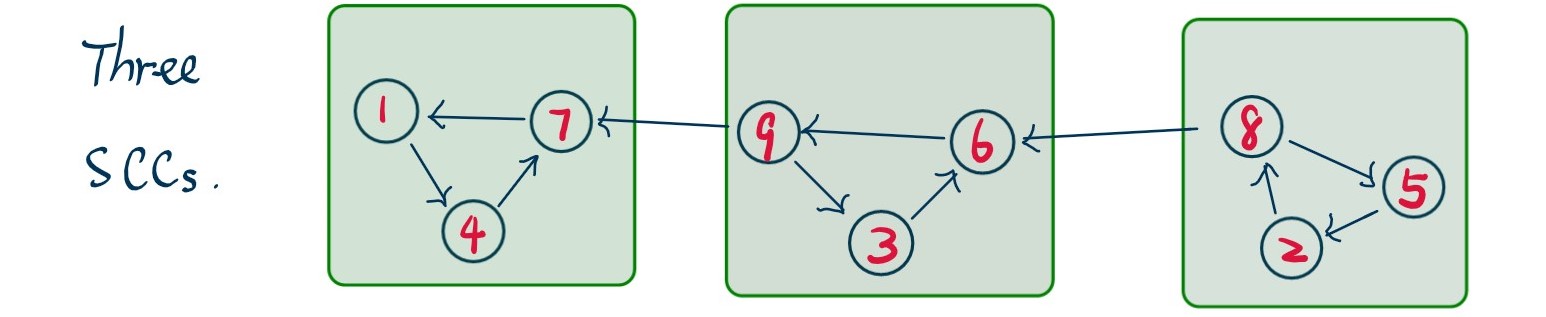
The question addressed in this post is to find the Strongly Connected Components (SCCs) in a directed graph G. These SCCs is a partition of G, which means SCCs are mutually disjoint non-empty subgraphs whose union is G. This is the first graph search question I’ve learned in the online courses, Algorithms: Design and Analysis. I decided to write a summary here because

1. the question is interesting;
2. it uses the stack data structure to accelerate the computation
3. the algorithm is blazingly fast with running time \(O(V + E)\), where \(V\) and \(E\) are the numbers of vertex and edge respectively.

Kosaraju’s algorithm is a two-pass algorithm. In the first pass, a Depth First Search (DFS) algorithm is run on the inverse graph to computing finishing time; the second pass uses DFS again to find out all the SCCs where the start note of each SCC follows the finishing time obtained in the first pass. The following analysis and code break the question into three pieces, reverse a directed graph, first DFS computing finishing time and second DFS finding SCCs.

Reverse a directed graph

Suppose the graph is represented by the adjacency list. 9: [7, 3] represents vertex with label 9 has two outgoing edges to the vertices with label 7 and 3.

1
2
3
4
5
6
7
8
9
10
11

adj_lst
defaultdict(list,
            {7: [1],
             4: [7],
             1: [4],
             9: [7, 3],
             6: [9],
             8: [6, 5],
             2: [8],
             5: [2],
             3: [6]})

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

from collections import defaultdict

class Graph:
    
    def __init__(self, adj_lst):        
        self.graph = adj_lst  
    
    def addEdge(self, vertex1, vertex2): # add an edge from vertex1 to vertex2
        self.graph[vertex1].append(vertex2)
    
    def reverseGraph(self):        
        inverseG = Graph(defaultdict(list))
        
        for i in self.graph:
            for j in self.graph[i]:
                inverseG.addEdge(j, i)
        return inverseG

First DFS computes finishing time

We randomly select a vertex and go along the directed edges as far as possible. The if we arrive at a vertex, who does not have an outgoing edge connecting to an unvisited vertex, we push the vertex to the stack and come back via the way we reach it. For instance, in the following reversed graph, we choose 9 => 6 => 3, since 3 does not have an outgoing edge connecting to any unvisited vertex, we push 3 to the stack and come back to 6. 6 still has another outgoing edge to 8. Then 6 => 8 => 2 \(\cdots\).

In the example, we proceed like:

• 9 => 6 => 3(push) => 6 => 8 => 2 => 5(push) => 2(push) => 8(push) => 6(push) => 9(push)
• 7 => 4 => 1 (push) => 4(push) => 7(push)

1
2
3
4
5
6
7
8
9
10
11
12
13

class Graph:
    
    def finishingTimeStack(self, vertex, visited, stack):
        '''
        visited: a dict to record visited vertices
        vertex: current vertex 
        stack: push vertex to stack as DFS proceeding
        '''
        visited[vertex] = True
        for i in self.graph[vertex]:
            if visited[i] == False:
                self.finishingTimeStack(i, visited, stack)
        stack.append(vertex)

Second DFS computes SCCs

After we get the finishing time via the first DFS, we change the name of notes to its finishing time in the original graph G. We are going to process the nodes from the highest label down to the lowest label 1. For both the first DFS and second DFS, to guarantee a visit of every note, an outer loop is necessary.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

class Graph:
    
    def getOneSCC(self, vertex, visited, scc):
        scc.append(vertex)
        visited[vertex] = True
        
        for v in self.graph[vertex]:
            if visited[v] == False:
                self.getOneSCC(v, visited, scc)
       
    def computeSCCs(self):
        
        stack = [] # order of stack is the finishing time
        
        ### First DFS: compute the finishing time
        visited = defaultdict(bool) # initialized all notes as unvisited
        
        for i in list(self.graph.keys()): # use outer loop to ganrantee every note will be visited
            if visited[i] == False:
                self.finishingTimeStack(i, visited, stack)
        
        ### Compute a inverse graph
        inverG = self.reverseGraph()
        
        ### Second DFS: compute the SCCs
        SCC_lst = []
        visited =  defaultdict(bool) # initialized all notes as unvisited 
        while stack:
            i = stack.pop()
            if visited[i] == False:
                scc = []
                inverG.getOneSCC(i, visited, scc)
                SCC_lst.append(scc)
        return SCC_lst

Run computeSCCs on the example

Note that in the given code, actually, we need to put the adjacent list of the inverse graph as the argument. This is because, in function finishingTimeStack, we compute the finishing time of the input adj_lst, not its inverse. And function computeSCCs compute the SCCs of the inverse of adj_lst.

1
2
3

oriG = Graph(adj_lst)
invG = oriG.reverseGraph()
invG.computeSCCs()

1

[[1, 4, 7], [9, 3, 6], [8, 5, 2]]

Note that if you use Python to run long recursion, please add the following code to manage stack size and recursion limit in Linux OS.

1
2
3
4
5

import resource
import sys

resource.setrlimit(resource.RLIMIT_STACK, (resource.RLIM_INFINITY, resource.RLIM_INFINITY))
sys.setrecursionlimit(2 ** 17)