Count inversion with merge sort

Question

Given a list of number, how many inversion pairs are there? If the list is [1, 3, 5, 2, 4, 6], there are three inversions: (3, 2), (3, 4), (3, 6). A brute force method would be using two loops, resulting in an algorithm with running time \( O(n^2) \), where \(n\) is the length of the list.

1
2
3
4
5
6

def bruteForceCount(arr):
    count = 0
    for i in range(len(arr)):
        for j in range(i + 1, len(arr)):
            if arr(i) > arr (j): count = count + 1
    return count 

Divide and Conquer

Can we do better?

The Merge sort algorithm using the Divide and Conquer technique reduces the running time from \(O(n^2)\) to \(n\log n\). From my understanding, the magic happens at the cleaning up step. With two length \(m\) sorted sublists, to form the original list, the running time is \(O(m)\) instead of \(O(m^2)\). Combined with the recursive tree structure, the depth of the tree is \(\log_2 n\) and running time for each level, \(i = 1, \ldots, \log_2 n\), is \(O(n)\). Finally, the merge sort algorithm has running time \(O(n\log n)\).

To count the inversion, the subquestion is to count the inversions in the left sublist and right sublist. The cleanup work is counting the number of split inversions, i.e, for inversion pair \((a, b)\), \(a \in\) left sublist and \(b \in\) right sublist. With two sorted length \(m\) sublists, the running time of the clean up work is \(O(m)\). Hence, the counting inversion algorithm has running time \(O(n\log n)\).

Statistical View

Where can we use this the algorithm? The inversion number can be used as a measurement of dissimilarity. For instance, if two customers give their ranking for 3 fruits, the number of inversions in rank lists will measure how their preference is different from each other.

Suppose that customer I ranks apple = 1, orange = 2, grape = 3. And customer II ranks orange = 1, grape = 2 and apple = 3. Then we count inversion of list [3, 1, 2] as 2. If they give the same rank list, the number of inversions is 0.

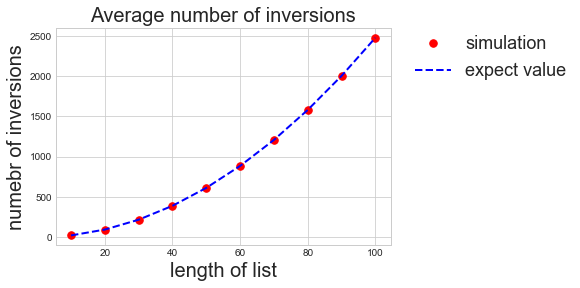
A nature question is if let two independent subjects rank \(n\) items, what is the average numebr of inversions. The answer is \(n(n-1)/4\). The following proof utilizes indicator function: \[I_{ij} = 1, \text{ if } i < j \text{ and } X[i] > X[j].\] Then number of inversions in the list \(\mathbf{X}\) is \(\sum_i\sum_j I_{ij}\). \[ \mathbf{E}\left(\sum_{i=1}^n\sum_{j=1}^n I_{ij}\right) = \sum_{i=1}^n\sum_{j=1}^n \mathbf{E}(I_{ij}) = \sum_{i=1}^n\sum_{j = i + 1}^n P(X[i] > X[j]) = \sum_{i=1}^n \sum_{j = i + 1}^n \frac{1}{2} = [(n-1)+\ldots+1]\times \frac{1}{2} = \frac{n(n-1)}{4},\] where the second equlity is due to the definition of expection of discrete random variable, and the reason for \(P(X[i] > X[j]) = 1/2\) is that when randomly picking up any two elements from the list, the first is greater than the second with probability 1/2.

Python Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

def mergeSortInversion(arr):
    
    # define base case
    if len(arr) == 1:
        return arr, 0
    else:
        # define two sublist
        left = arr[:int(len(arr)/2)]
        right = arr[int(len(arr)/2):]
        
        # recursion, return left and right are the sorted sublists
        left, leftCount = mergeSortInversion(left)
        right, rightCount = mergeSortInversion(right)
        
        # the sorted list
        lsorted = []
        
        i = 0 # index of left sublist
        j = 0 # index of right sublist
        inversions = leftCount + rightCount
        
        while i < len(left) and j < len(right):
            if left[i] <= right[j]:
                # not an inversion
                lsorted.append(left[i])
                i = i + 1
            else:
                # an inversion case
                lsorted.append(right[j])
                j = j + 1
                inversions = inversions + len(left) - i
         
        # conbime the remaining sublist, note only one of left[i:] and right[j:] is not null
        lsorted = lsorted + left[i:]
        lsorted = lsorted + right[j:]

    return lsorted, inversions 

Simulation

Now we run a small simulation to estimate the average number of inversions in a length \(n\) list.

1
2
3
4
5
6
7
8
9
10
11
12
13
14

import numpy as np

mlist = np.arange(1, 11)*10
totalCountlist = []

for m in mlist:
    totalCount = 0
    for i in range(1000):
        arr = np.random.permutation(m)
        arr = arr.tolist()
        arrsot, cot = mergeSortInversion(arr)
        totalCount = totalCount + cot
        aveCount = totalCount/1000
    totalCountlist.append(aveCount)

Average number of inversions as a function of length \(n\):